$\pi$ 应该是我们最熟悉的数学常数了,但是除了 $\pi$ 以外,还有一个数学常数 $e$,它同样重要,同样与我们生活息息相关,甚至被冠名为 自然常数,它是对数函数的底数,有时候也称它为欧拉数(Euler number),以瑞士数学家欧拉命名。
它的一个数学定义是这样的:
$$
e = \lim\limits_{n \to \infty} (1+\frac{1}{n})^n
$$
其数值约等于(小数点后25位): 2.71828 18284 59045 23536 02874
相信大家前段时间都玩过或听过《荒野乱斗》这个游戏,我司前端大佬 Fred 哥也一直在为升杯而努力,玩这个游戏很大的一个动力是攒个宝箱开个英雄出来。

假设现在有一个超级宝箱,它开出英雄的概率是 0.1%(1/1000),千分之一。我们的 Fred 哥又很有钱,那他氪金氪它个 1000 发,是不是一定能开出个英雄来?基于我们的数学常识,明显不是的。
那么我们可不可以求一下 Fred 哥倒霉的概率呢?他买了 1000 个超级宝箱,一个英雄都没开出的概率是多少呢?
一个超级宝箱,它开出英雄的概率是 0.1%(1/1000),那开不出英雄的概率就是:
$$
1-\frac{1}{1000}
$$
第一次开不中概率是 $(1-\frac{1}{1000})$,那两次开不中的概率是 $(1-\frac{1}{1000})(1-\frac{1}{1000})$ ,以此类推,那开 1000 个宝箱都不中的概率是:
$$
(1-\frac{1}{1000})^{1000} \approx 0.36769542477096404462680613922046134399
$$
乍一看,好像跟我们的 $e$ 没啥联系啊。
但是如果我们把 0.367695424770964044626... 这个值倒转一下:
$$
\frac{1}{0.367695424770964044626..} \approx 2.71964221644285036539755346440401494764
$$
怎么样?结果的 2.719642216442... 这个数值是不是似曾相识?这非常接近我们的自然常数 $e$ 的值。
如果宝箱开出英雄的概率变成 0.01%,万分之一,Fred 哥买的宝箱数目也增大到一万个,那这个值又会如何变化呢:
$$
(1-\frac{1}{10000})^{10000} \approx 0.3678610464329299241113356722185087445
$$
$$
\frac{1}{0.3678610464329299241113356722185087445} \approx 2.7184177550104492651837311208355930494
$$
如果继续将开出英雄的概率变低,Fred 哥买的宝箱数目也相应变大,最后结果是怎样的呢?我们先构造这样一个式子来计算:
$$
\frac{1}{(1-\frac{1}{n})^n}
$$
接着利用 Swift Playground 来计算其结果,观察随着 n 变大,最后的结果是怎样变化的:
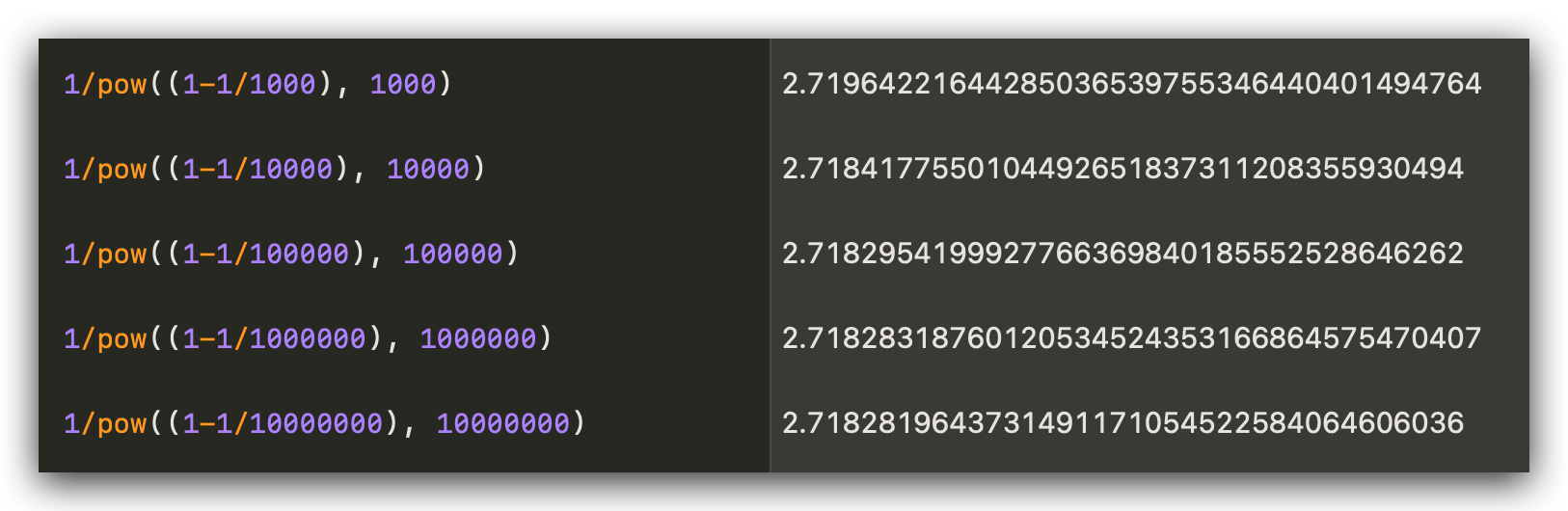
我们可以发现,随着 n 越来越大,最后的值会越来越接近 $e$ 的值!我们可以用下面这个极限的式子表示:
$$
\lim\limits_{n \to \infty} (1-\frac{1}{n})^n = \frac{1}{e}
$$
扩展一下:
如果我们把前面说到的超级宝箱例子,具象成一个装满球的箱子,假设箱子里有 1000 个球,我们每次有放回地抽取一个球,抽取 1000 次,那么最后没有被抽到的球大概有多少个呢?答案是 368 个。
这里的计算其实与上面的几乎一样,求出没有被抽到球的概率,然后乘以球的总数:
$$
(1-\frac{1}{1000})^{1000} \approx 0.368
$$
$$
1000 \times 0.368 = 368
$$
这个在统计学上,这个其实叫做自助抽样法(Bootstrapping Method) : 是一种从给定训练集中有放回的均匀抽样,也就是说,每当选中一个样本,它等可能地被再次选中并被再次添加到训练集中。
从数量为 N 的样本中「有放回地」随机抽取出一个「数量同样为N」的样本,那么理论上来说,原来的 N 个个体中大约会有
36.8%的个体不会被抽中。(引用来源)
这种抽样方法已经应用在很多领域,比如在机器学习领域,大家都略有耳闻的 随机森林 算法,就是在训练集中利用这种抽样方式,从原始训练样本集 N 中有放回地重复随机抽取 N 个样本生成新的训练样本集合训练决策树,然后没有被抽中的 36.8% 作为 Out of Bag 数据集训练,即袋外误差来验证决策树。具体就不展开讲了,因为我也不是很懂 :-)
我们回到 Fred 哥身上,前文提到 Fred 哥很有钱,但是有一天 Fred 哥居然找我借了 100 块钱,我很无耻地定了 100% 的年息利率。也就是一年后我可以得到 200 块:
$$
100 \times (1 + 100\%) = 200
$$
但是这时候我想起了复利的概念,如果仍然保持 100% 的年利率,但是我半年结一次息,把得到的利息和加入100块里,让它利滚利,也就是说每半年的利率为 $\frac{100\%}{2} = 50\%$ 那这样的话,一年后我可以得到 225 块:
$$
100 \times (1+\frac{100\%}{2}) \times (1+\frac{100\%}{2}) = 225
$$
看起来复利真不错啊!丧心病狂的我决定从半年结一次息改成每个季度结一次息,一年后我可以得到 244 块:
$$
100 \times (1+\frac{100\%}{4})^4 \approx 244
$$
太棒了,又多了点钱,贪得无厌的我决定每个月结一次息,不,我要每天结一次息,我要半天结一次息,我要每小时结一次息,我要每分钟结一次息,我要每秒结一次息…… 被连续复利冲昏头脑的我想着这次要彻底榨干 Fred 哥!兴奋的我,又打开了 Swift Playground,喜滋滋地让程序帮我算出最后能得多少钱:
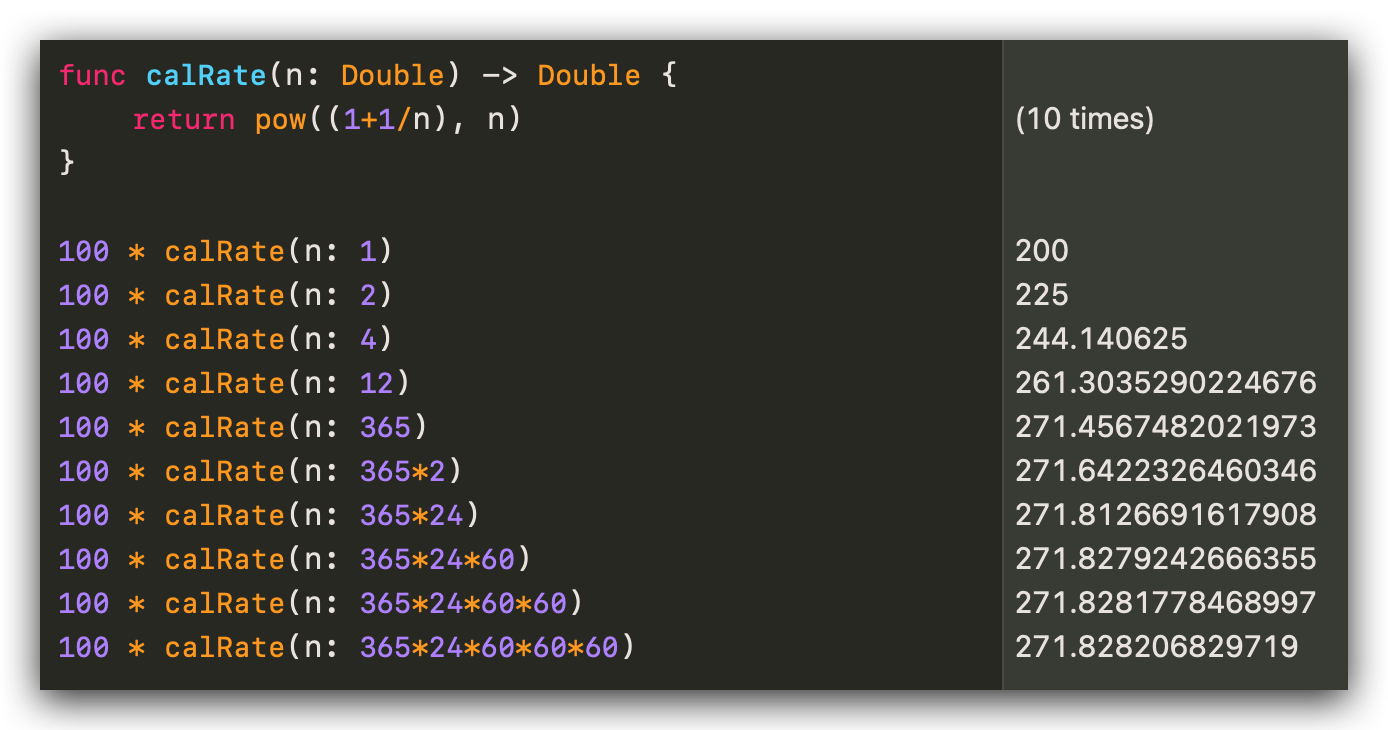
咦!发生什么情况,怎么随着结息次数的增加,钱怎么都不往上涨了??而且越来越趋向 271.828 。
这个数字是不是似曾相识?没错,这个值就是 $e \approx 2.71828$ 乘以 100 所得到,也就是不管结息次数怎么增大,最后得到的钱也只能是 $e$ 倍!因此也有人说 $e$ 是在一个特定周期内的增长极限。
这里我们祭出一个关于极限的公式:
$$
\lim\limits_{n \to \infty} (1+\frac{1}{n})^n = e
$$
通过上面的例子,大家应该能体会 $e$ 是多么神奇的一个数学常数。$e$ 在我们生活中可以说无处不在,除了这些纯数学上的例子外,自然界中很多东西也和 $e$ 有关。比如等角螺线,或者称对数螺线、生长螺线。
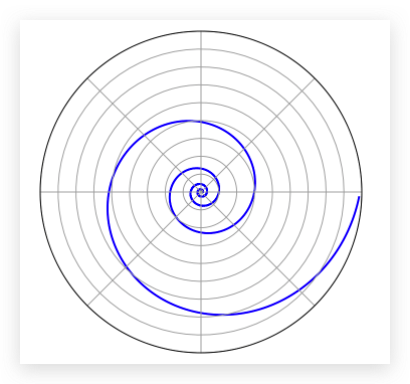
它是自然界中常见的螺线,在极坐标系 $(r, \theta)$ 中,这个曲线的公式可以写成:
$$
r = ae^{b\theta}
$$
从公式可以看到,我们的 $e$ 又出现了。还真的是无处不在啊。
下面举一下自然界中的例子(来自维基百科:等角螺线):
| 鹦鹉螺的贝壳像等角螺线 |  |
| 菊的花蕊排列成等角螺线 |  |
| 鹰以等角螺线的方式接近它们的猎物 | |
| 昆虫以等角螺线的方式接近光源 | |
| 蜘蛛网的构造与等角螺线相似 |  |
| 旋涡星系的旋臂差不多是等角螺线。银河系的四大旋臂的倾斜度约为 12°。 |  |
| 低气压(热带气旋、温带气旋等)的外观像等角螺线 |  |
最后点一下题吧,这些自然的现象,都与等角螺线有关,也就是都跟我们的自然常数 $e$ 有关。小至游戏宝箱,大至宇宙星系,都有 $e$ 存在的身影。$e$ 称之为自然常数,当之无愧。




