如何判别凹多边形

问题描述

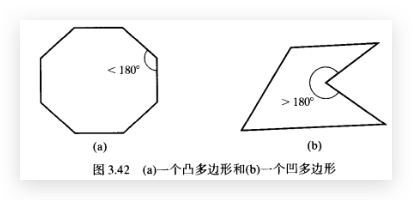
如何判断一个多边形是否为凹多边形？首先我们先要明确凹多边形是如何定义的，以及它的特征。

在 《计算机图形学》 的 3.15.1 多边形分类 这一小节里有这样的描述：

多边形的一个内角是由两条相邻边形成的多边形边界之内的角。如果一个多边形的所有内角均小于180°，则该多边形为凸 (convex) 多边形。… 不是凸多边形的多边形称为凹 (concave) 多边形。如下图:

接着在 3.15.2 识别凹多边形 这一小节里，简单地描述了通过多边形边向量叉积的方法来判断多边形是否为凹多边形：

如果为多边形每一边建立一个向量，则可使用相邻边的叉积来测试凸凹性。凸多边形的所有向量叉积均同号。因此，如果某些叉积取正值而另一些为负值，可确定其为凹多边形。

接着该小节也给出了网上流传甚广，却很少说明出处的一张图来解释边向量叉积的方法：

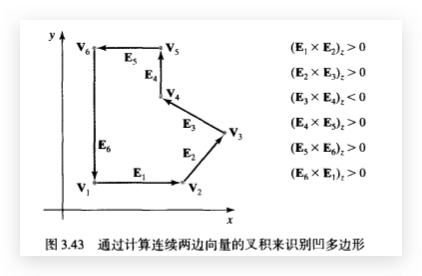
如果没有相关知识背景的人，看到这里可能会有点懵。为什么从凹多边形存在内角大于 180 度这一特征，能引出边向量的同向性的方法来判断凹多边形？这里的思路转化是怎么样的？下面以我粗浅的理解来给大家说说。

理解边向量叉积方法

1. 移动边向量

首先我们绘制一个简单的凸多边形：[P0, P1, P2, P3, P4]，然后从第一个点 P0 开始，将每两个点组成的线段作为一个向量，方向为按照组成多边形的点的顺序方向，如下图所示：

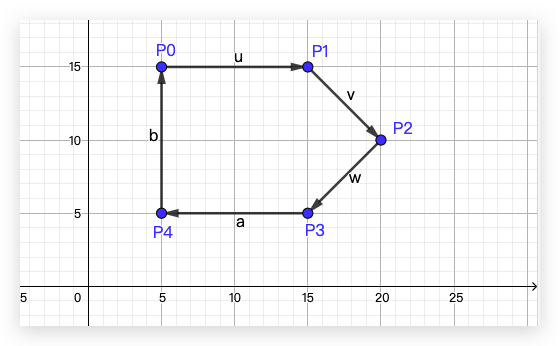
接着，保持向量的大小和方向不变，将所有边向量的起点移动到坐标系的原点：

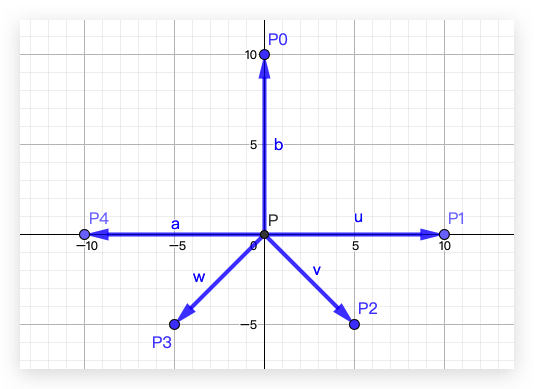
我们可以观察到向量 u、v、w、a、b 呈现的是顺时针的顺序。这个现象很重要，在继续之前我们先回顾一下向量叉积的知识。

2. 回顾叉积

我们只需知道叉积的结果是有正负的，比如我们以向量 $\vec{v}$ 为标准，有如下特征：

向量 $\vec{w}$ 在 $\vec{v}$ 的 顺时针方向，那么 $\vec{v} \times \vec{w} < 0$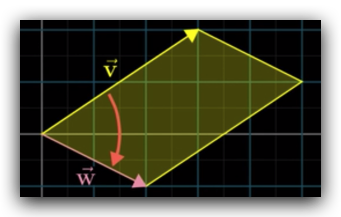
如果向量 $\vec{w}$ 在 $\vec{v}$ 的 逆时针方向，那么 $\vec{v} \times \vec{w} > 0$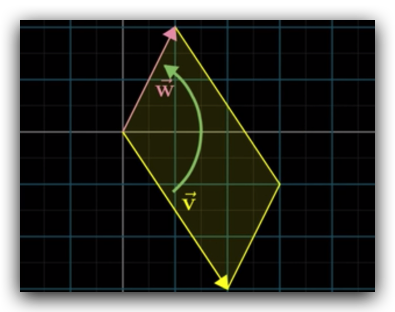

3. 凸多边形边向量叉积均同号

上面我们将一个凸多边形的边向量的起点都移动到了坐标原点，发现所有的向量都是按照顺时针的顺序呈现的。

结合向量叉积的知识，我们可以得出：所有边向量按顺序两两进行叉积，得出的结果都是小于 0 的，即该凸多边形的所有边向量叉积均同号：
$$
\vec{u} \times \vec{v} < 0 \
\vec{v} \times \vec{w} < 0 \
\vec{w} \times \vec{a} < 0 \
\vec{a} \times \vec{b} < 0 \
$$
那么，如果是凹多边形会是怎么样呢？

4. 凹多边形边向量叉积不同号

同样的，我们把一个凹多边形的边向量也移动到坐标原点进行观察：

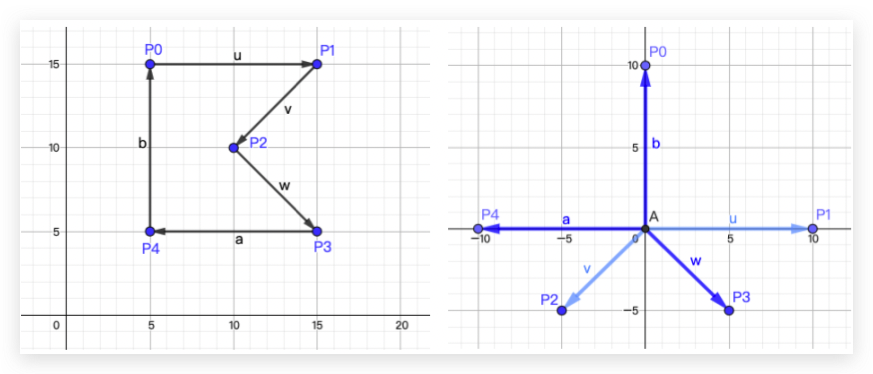
如上图，凹多边形 [P0, P1, P2, P3, P4]，观察其移动后边向量，会发现向量 u、v、w、a、b 并不是严格按照顺时针顺序的。 $\vec{w}$ 出现在 $\vec{u}$ 和 $\vec{v}$ 之间。

那么如果所有边向量按顺序两两进行叉积，得出的结果就会出现不同号的情况：
$$
\vec{u} \times \vec{v} < 0 \
\vec{v} \times \vec{w} > 0 \
\vec{w} \times \vec{a} < 0 \
\vec{a} \times \vec{b} < 0 \
$$

正是因为凹多边形内存在大于180度的内角，导致凹多边形失去了凸多边形才有的边向量同号特性，因此我们可以利用这一特性来判别多边形是凹还是凸。

5. 代码实现判别凹多边形

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

/// 判断是否凹多边形
/// 凸多边形的所有边的向量叉积均同号，一个多边形的所有边向量的叉积结果存在不同号,则可判定其为凹多边形
func isConcavePolygon(vertexs: [CGPoint]) -> Bool {
    var allLines = [(CGPoint, CGPoint)]()
    // 根据前后两点确定所有线段
    for (pointIndex, point) in vertexs.enumerated() {
        let p1 = point
        let p2 = vertexs[(pointIndex + 1) % vertexs.count]
        allLines.append((p1, p2))
    }

    // 计算前后两邻边向量叉积，判断是否凹多边形
    var preValue = crossproduct(vector1: allLines[0], vector2: allLines[1])
    for lineIndex in 1..<allLines.count {
        let current = allLines[lineIndex]
        let next = allLines[(lineIndex + 1) % allLines.count]
        let currentValue = crossproduct(vector1: current, vector2: next)
        // 如果当前两邻边叉积与上两邻边叉积不相等，即不同号，则为凹多边形
        if preValue != currentValue {
            return true
        }
        preValue = currentValue
    }

    return false
}

func crossproduct(vector1: (CGPoint, CGPoint), vector2: (CGPoint, CGPoint)) -> CGFloat {
    let p1 = vector1.0
    let p2 = vector1.1
    let q1 = vector2.0
    let q2 = vector2.1

    let crossproduct = (p2.x - p1.x) * (q2.y - q1.y) - (q2.x - q1.x) * (p2.y - p1.y)

    return crossproduct >= 0 ? 1 : -1
}