为什么OpenGL里旋转等变换矩阵是4x4的矩阵

Hanson

OpenGL

发布于：Oct 23, 2020

OpenGL ES 的很多教程里都会有这样一个例子来讲解纹理：将一张图片作为纹理显示在屏幕上。

因为纹理坐标和实际屏幕显示的坐标不一样，把图片渲染在屏幕上后，图片是上下颠倒的。

一个解决方法是对当前的顶点坐标，乘以绕 z 轴旋转180度的矩阵，这样图片就能正确显示了。

$$
\begin{bmatrix}
cos\theta & -sin\theta & 0 & 0 \\ sin\theta & cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \
\end{bmatrix}
$$

那么如何理解这个旋转矩阵呢？

影响我们理解这个矩阵的第一个问题是：

为什么这个矩阵是 4x4 的？ 而且我们发现旋转，缩放、平移等变换矩阵都是 4x4 的。

在直观上的认知里，表达一个三维空间的坐标用 x,y,z 就足够了，那在三维空间里进行矩阵变换，用 3x3 的矩阵就够了，为什么需要 4x4 呢？

为了回答这个问题，下面我们先在几何意义上理解向量和矩阵之间的关系，然后通过推导旋转矩阵和平移矩阵，一步步来解开这个疑惑。

向量和矩阵

在几何平面上，我们可以把平面上任意一点，当作与原点组成的一个 向量 来理解。

如图，A 点可以表示成向量 $\vec{OA}$ ；在 x 轴和 y 轴上各有 i 点（1， 0）和 j 点（0，1），同样的，让它们与原点组成向量，为了简化，我们用 $\vec{i}$ 和 $\vec{j}$ 表示这两个向量。

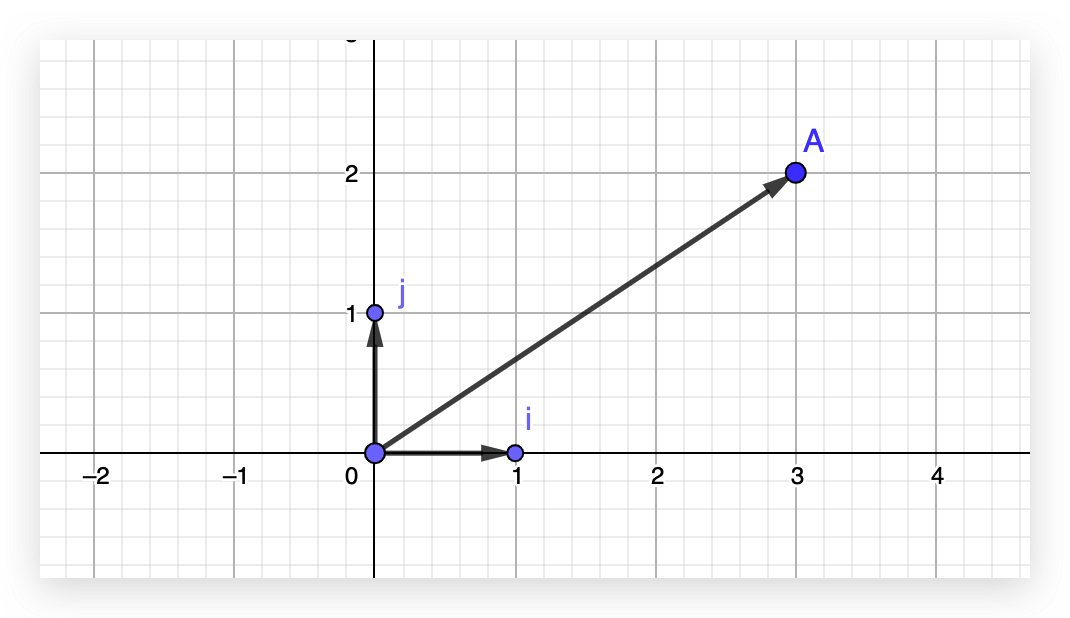
因为 A 点的坐标为 (3, 2)，如果我们要用 $\vec{i}$ 和 $\vec{j}$ 表示 $\vec{OA}$ ，那是这样的：
$$
3\vec{i} + 2\vec{j} = \vec{OA}
$$
这里的几何意义是 $\vec{i}$ 延展到 $3\vec{i}$ ，$\vec{j}$ 延展到 $2\vec{j}$ ，然后把这两个向量相加即可得到 $\vec{OA}$

i 坐标是（1， 0），j 坐标是（0，1），我们把上面这个等式转换成竖列的形式：
$$
3
\begin{bmatrix}1\\0\end{bmatrix}
+
2
\begin{bmatrix}
0\\1
\end{bmatrix}
=
\begin{bmatrix}
3 \\ 2
\end{bmatrix}
$$
这里其实是向量的简单运算，运算过程如下：
$$
\begin{bmatrix}
3 \times 1 \\ 3 \times 0
\end{bmatrix}
+
\begin{bmatrix}
2 \times 0\\2 \times 1
\end{bmatrix}
=
\begin{bmatrix}
3 \times 1 + 2 \times 0\\3 \times 0 + 2 \times 1
\end{bmatrix}
=
\begin{bmatrix}
3\\2
\end{bmatrix}
$$
看到运算过程是否有种似曾相识的感觉？这不就是矩阵与向量的乘法计算吗？这个运算其实就是将向量左乘一个矩阵 的计算：
$$
\begin{bmatrix}
1 & 0\\0 & 1
\end{bmatrix}
\begin{bmatrix}
3\\2
\end{bmatrix}
=
\begin{bmatrix}
3 \times 1 + 2 \times 0 \\3 \times 0 + 2 \times 1
\end{bmatrix}
=
\begin{bmatrix}
3 \\ 2
\end{bmatrix}
$$
这里 $\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$ 其实就是单元矩阵，左乘一个单元矩阵并不会改变原来的值。而这个单元矩阵以两个竖列来看，正是 i 和 j 点的坐标，也是向量 $\vec{i}$ 和 $\vec{j}$ ，在数学上将 $\vec{i}$ 和 $\vec{j}$ 称为此坐标系的 基向量。

推导旋转矩阵

我们现在把整个坐标轴绕原点逆时针旋转 $45^o$ ：

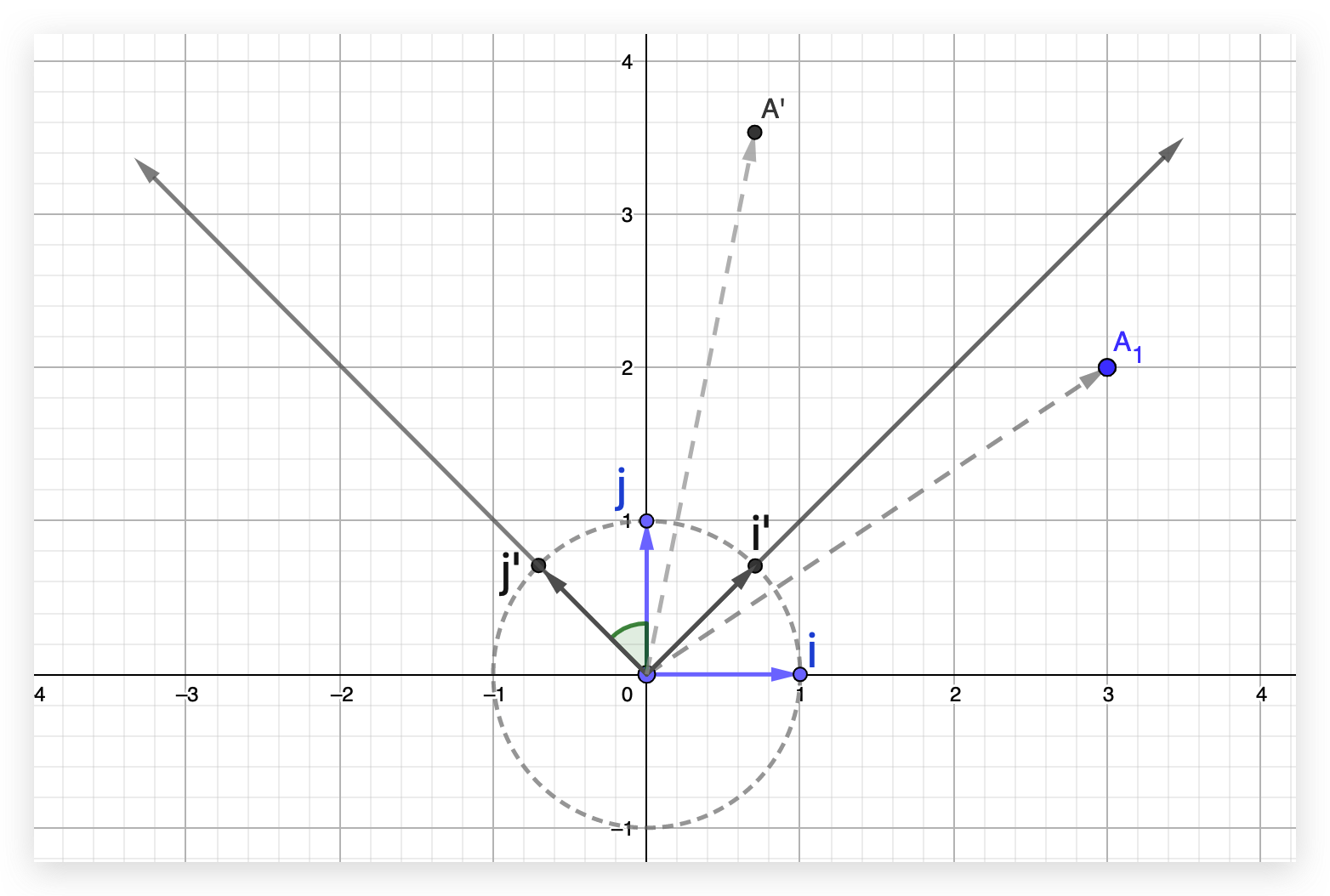
旋转后 i 点和 j 点对应 $i^\prime$ 和 $j^\prime$ 位置。

通过简单的三角函数计算得到： $i^\prime$ 坐标为 $\begin{bmatrix}cos45^o \\ sin45^o\end{bmatrix}$ ，$j^\prime$ 坐标为 $\begin{bmatrix} -sin45^o \\ cons45^o \end{bmatrix}$

旋转后，A 点的坐标是多少呢？回顾上面的做法， $\vec{i^\prime}$ 延展到 $3\vec{i^\prime}$ ，$\vec{j^\prime}$ 延展到 $2\vec{j^\prime}$ ，然后把这两个向量相加即可得到 $\vec{OA^\prime}$ 。结合上面一节矩阵和向量的推演，可以变成下面的形式：
$$
\begin{bmatrix}
cos45^o & -sin45^o \\sin45^o & cos45^o
\end{bmatrix}
\begin{bmatrix}
3 \\ 2
\end{bmatrix}
$$
我们发现，左边的矩阵不正是开头所看到的 旋转矩阵 吗？只不过这是二维平面上的旋转矩阵:
$$
\begin{bmatrix}
cos\theta & -sin\theta \\sin\theta & cos\theta
\end{bmatrix}
$$
结合图形和计算，我们可以这样理解这个二维矩阵：二维矩阵代表一个坐标系里的两个基向量，而在这个坐标系里的点与原点组成的向量，都可以用这两个基向量的变换来表示。那么旋转一个点，可以转换成旋转这个点所在的坐标系，从而通过变化的基向量求出旋转后的点的位置。

其实这种变换在数学上称作 线性变换 ，线性变换是通过 矩阵乘法 来实现

线性变换：是在两个向量空间（包括由函数构成的抽象的向量空间）之间的一种保持向量加法和标量乘法的特殊映射

线性变换在几何直观上有如下特点：

变换前后，直线仍然保持是直线的状态

变换前后，原点保持固定，不会变化

我们从二维平面，推导到三维坐标也是同理，只不过是多了个 z 轴
$$
\begin{bmatrix}
1 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 1
\end{bmatrix}
$$
竖着来看这个矩阵，是 x，y，z轴上的三个基向量，同时它又是一个单元矩阵。

同理上面二维平面的推导，三维坐标绕 z 轴的旋转矩阵为：
$$
\begin{bmatrix}
cos\theta&-sin\theta&0\\sin\theta&cos\theta&0\\0&0&1
\end{bmatrix}
$$

推导平移矩阵

那么平移操作，能不能也用这种矩阵与向量相乘的形式呢？我们再次回到二维平面，看看将 A 点平移到 B 点的情况是怎样的。

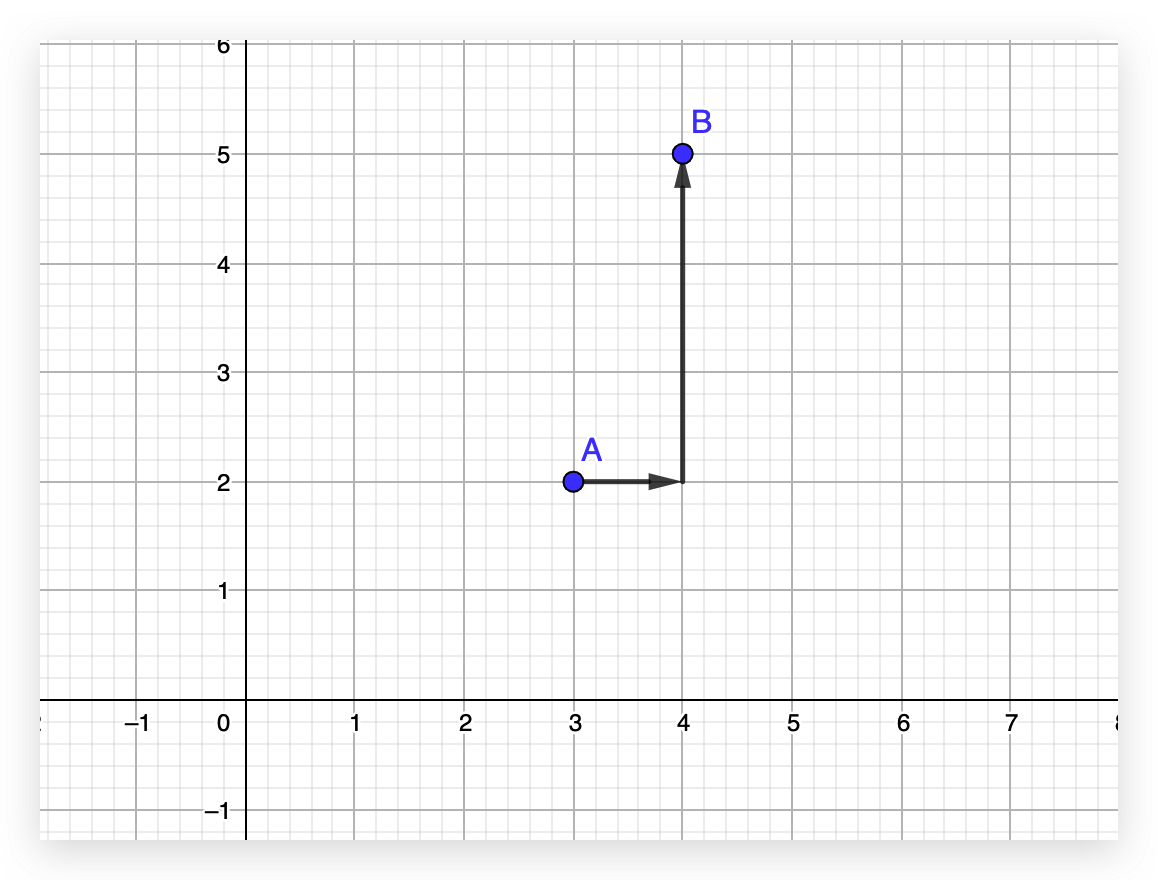
要将 A 点（3，2）平移到 B 点(4，5)，实际上就是先将 A 点往右移动 1 ，再往上移动 3，即 x 坐标值增加 1，y坐标值增加 3
$$
\begin{bmatrix}
x + 1 \\ y + 3
\end{bmatrix}
=
\begin{bmatrix}
x \\ y
\end{bmatrix}
+
\begin{bmatrix}
1 \\ 3
\end{bmatrix}
=
\begin{bmatrix}
3 + 1 \\ 2 + 3
\end{bmatrix}
=
\begin{bmatrix}
4 \\ 5
\end{bmatrix}
$$
从上面的运算来看，平移这种操作实际上是 向量的加法，即:
$$
\vec{OA} + \vec{OC} = \vec{OB}
$$

$$
\begin{bmatrix} 3 \\ 2 \end{bmatrix} + \begin{bmatrix} 1 \\ 3 \end{bmatrix}=\begin{bmatrix} 4 \\ 5 \end{bmatrix}
$$

我们可以通过向量加法的 平行四边形法则 加深理解，如下图：

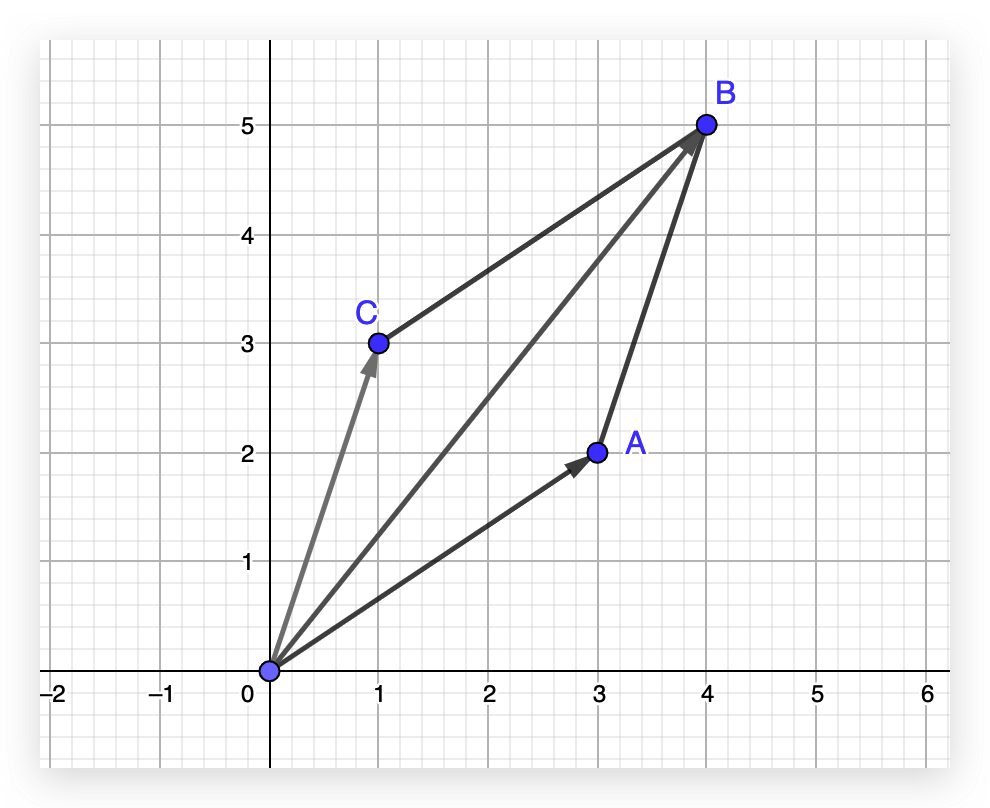
对于平移这种操作，我们无法仅仅通过矩阵乘法来实现。

而实际上，平移这种操作属于 仿射变换 。

仿射变换，又称仿射映射，是指在几何中，对一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。

仿射变换在几何直观上，相比线性变换，它不需要保证变换前后坐标原点不变。

如下图，从 A 点平移到 B 点，我们换一个角度思考，这次不移动点，而是移动整个坐标轴，同样可以达到平移 A 点到 B 点的需求，但是坐标原点移动到了 O’ 点（1，3）。

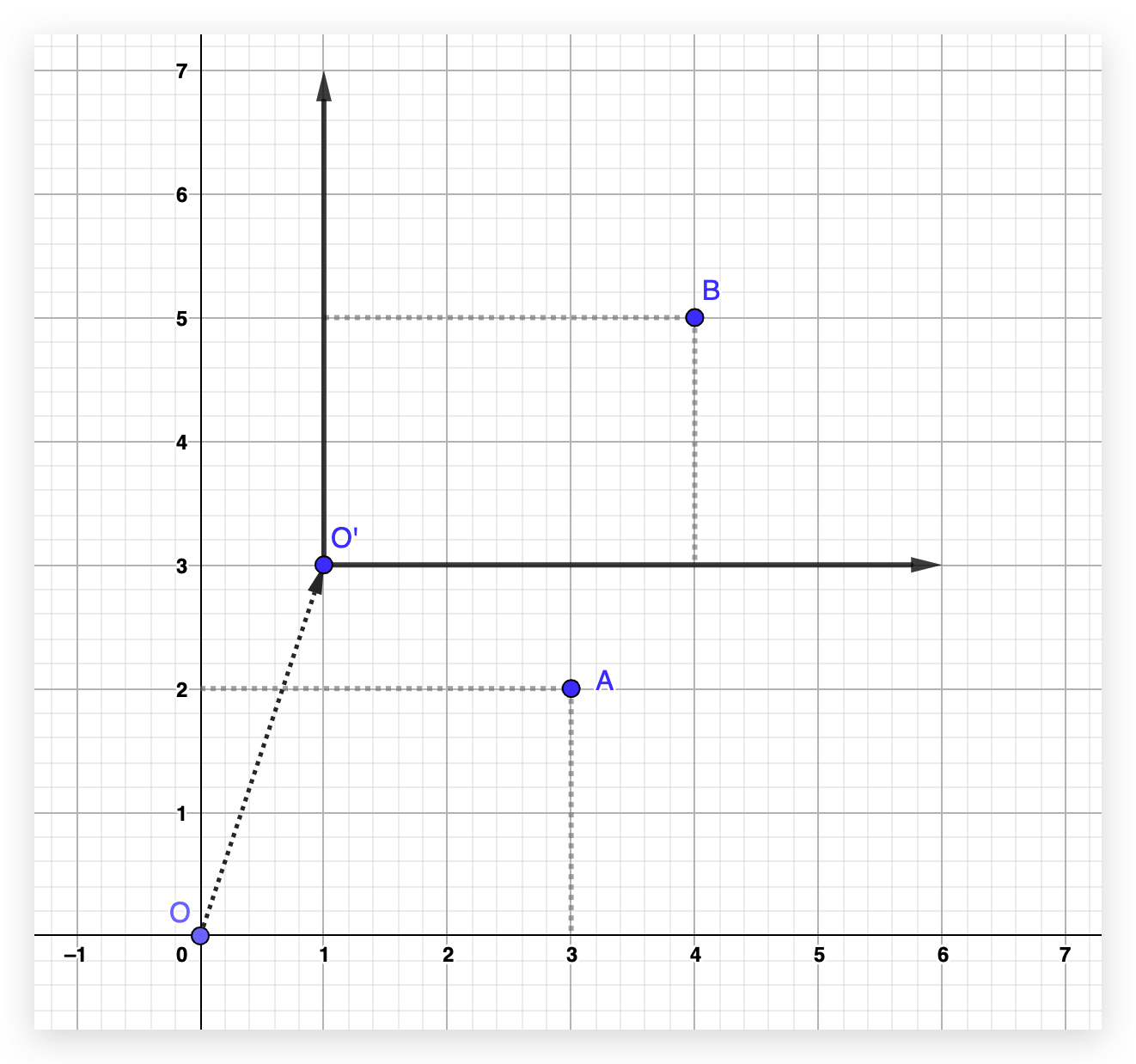
我们希望构造的是像下面这种矩阵乘法的等式，这样才能用一个通用的计算模式来处理坐标点的变换。
$$
\begin{bmatrix}
矩阵
\end{bmatrix}
\begin{bmatrix}
3\\2
\end{bmatrix}
=
\begin{bmatrix}
4\\5
\end{bmatrix}
$$
到这里，我们终于要请出 齐次坐标 了。

齐次坐标就是将一个原本是 n 维的向量用一个 n+1 维向量来表示，是指一个用于投影几何里的坐标系统，如同用于欧氏几何里的笛卡儿坐标一般。

用一个通俗的讲法是，我们需要 升维 来处理这个问题。

通过增加一个维度，我们可以在高维度上，通过线性变换来处理低维度的仿射变换。

这句话咋一听感觉很有哲理，但是通过下面的数学等式就能知道其中的奥妙：
$$
\begin{bmatrix}
1 & 0 & 1 \\0 & 1 & 3 \\0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
3 \\ 2 \\ 1
\end{bmatrix}
=
\begin{bmatrix}
1 \times 3 + 0 \times 2 + 1 \times 1 \\0 \times 3 + 1 \times 2 + 3 \times 1 \\0 \times 3 + 0 \times 2 + 1 \times 1
\end{bmatrix}
=
\begin{bmatrix}
4 \\ 5 \\ 1
\end{bmatrix}
$$
观察上面的运算过程，结果 $\begin{bmatrix}4\\5\\1 \end{bmatrix}$ 不正是我们上面所得的 $\begin{bmatrix} 4\\5 \end{bmatrix}$ 吗？只不过多了一个 z 轴的坐标值。

我们通过升级一个维度，将在二维平面上的平移问题转换成了在三维坐标的矩阵和向量乘法。那么在二维平面上，这个平移矩阵就为：
$$
\begin{bmatrix}
1 & 0 & tx \\0 & 1 & ty \\0 & 0 & 1
\end{bmatrix}
$$
tx 和 ty 就对应在 x 轴和 y 轴上的移动距离。

同理推广到三维坐标系，要实现三维坐标的平移操作，同样需要通过升维，引入齐次坐标来计算。那么三维坐标下的平移矩阵就为：
$$
\begin{bmatrix}
1 & 0 & 0 & tx \\0 & 1 & 0 & ty \\0 & 0 & 1 & tz \\0 & 0 & 0 & 1 \
\end{bmatrix}
$$